Understanding Binary Search, A Comprehensive Guide

Binary search is a fundamental algorithm used in computer science for searching elements in sorted arrays or lists. Its efficiency and simplicity make it a widely used and essential tool in programming, especially when dealing with large datasets.

In this article, we will delve into the concept of binary search, exploring its principles, implementation, and applications. Whether you’re a beginner looking to understand the basics or an experienced programmer seeking a refresher, this guide aims to provide a comprehensive overview of binary search.

We’ll start by explaining the underlying principles of binary search, followed by a detailed breakdown of its implementation in various programming languages. Additionally, we’ll explore the time complexity of binary search and discuss its advantages and limitations compared to other search algorithms.

Furthermore, we’ll showcase practical examples and use cases where binary search shines, including searching in arrays, finding specific elements in sorted lists, and determining boundaries or thresholds in real-world scenarios.

By the end of this article, you’ll have a solid understanding of binary search and its significance in algorithmic problem-solving. Whether you’re tackling coding challenges, optimizing performance in your applications, or simply expanding your programming knowledge, mastering binary search is a valuable skill that will serve you well in your journey as a programmer. So, let’s dive in and unlock the power of binary search together!

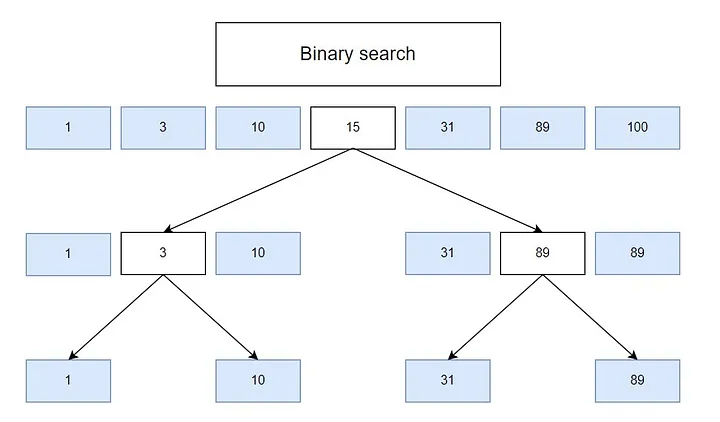
Binary search is a divide and conquer algorithm. It repeatedly divides the search interval in half and narrows down the possible locations of the target value.

Binary search is highly efficient with a time complexity of O(log n), where n is the number of elements in the array. It eliminates half of the remaining elements in each step of the search.

Algorithm:

Begin with defining two pointers, left and right, representing the start and end of the search interval respectively. Calculate the middle index of the search interval as (left + right) / 2. Compare the middle element of the array with the target value.

• If the middle element is equal to the target, return its index.
• If the middle element is greater than the target, update right to middle — 1 to search in the left half.
• If the middle element is less than the target, update left to middle + 1 to search in the right half.
• Repeat the process until the target is found or the search interval is empty (left is greater than right).

Binary search implementation on Java

public class BinarySearch {
    public static int binarySearch(int[] arr, int target) {
        int left = 0;
        int right = arr.length - 1;

        while (left <= right) {
            int mid = left + (right - left) / 2;

            // Check if the target is found at the middle
            if (arr[mid] == target) {
                return mid;
            }
            
            // If the target is greater, ignore left half
            else if (arr[mid] < target) {
                left = mid + 1;
            }
            
            // If the target is smaller, ignore right half
            else {
                right = mid - 1;
            }
        }
        
        // If the target is not found in the array
        return -1;
    }

    public static void main(String[] args) {
        int[] arr = {1, 2, 3, 4, 5, 6, 7, 8, 9};
        int target = 5;
        int result = binarySearch(arr, target);
        if (result != -1) {
            System.out.println("Element " + target + " is present at index " + result);
        } else {
            System.out.println("Element " + target + " is not present in the array");
        }
    }
}

This implementation may seem straightforward at first glance, but it introduces complexity due to the need for adjustments such as

right = middle - 1 and left = middle + 1

These adjustments can be confusing, making the code harder to understand. However, we can simplify the implementation by adopting a different approach. By visualizing the search range as [left, right), we can streamline our code, in other words we using half interval.

Key observations:

Searched value is always located in [l, r — 1], hence the main cycle exit condition is:

l == r - 1 or l + 1 == r

Also from this interpretation hence that next condition is always true:

a[r] > x

Where x is target value and a[r] the most right element in our segment.

The revised implementation presented below demonstrates this approach, resulting in clearer and more concise code:

public class BinarySearchExample {

    private int binarySearch(int[] array, int target) {
        int left = 0;
        int right = array.length - 1;
        
        while (left + 1 < right) {
            int middle = (left + right) / 2;
            
            if (array[middle] >= target) {
                right = middle;
            } else {
                left = middle;
            }
        }
        
        return array[left + 1] == target ? left + 1 : -1;
    }

    public static void main(String[] args) {
        BinarySearchExample example = new BinarySearchExample();
        
        int[] array = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19};
        int target = 11;
        
        int resultIndex = example.binarySearch(array, target);
        
        if (resultIndex != -1) {
            System.out.println("Target " + target + " found at index " + resultIndex);
        } else {
            System.out.println("Target " + target + " not found in the array");
        }
    }
}

Binary search is easy understand algorithm. But applying it takes time. Try to solve the next problems to study this useful algorithm.

https://leetcode.com/problems/binary-search/

• Ensure that the input array is sorted.
• Implement the binary search algorithm to efficiently find the target element in the array.
• Carefully handle cases where the target element may not be present in the array.

https://leetcode.com/problems/sqrtx/

• Define the search interval appropriately to ensure that the square root is found within the range [0, x]

https://leetcode.com/problems/find-k-closest-elements/

• Find the closest element. Once the closest element is found, use a two-pointer approach to find the K closest elements around it.
• Handle edge cases such as when K is greater than the number of elements in the array.

https://leetcode.com/problems/koko-eating-bananas/

• Use binary search to find the minimum possible value of eating speed that allows Koko to eat all bananas within the given time limit.
• Define the search interval based on the range of possible eating speeds.
• Consider the constraints carefully, such as the maximum speed at which Koko can eat bananas.

https://leetcode.com/problems/find-peak-element/

• Define the search interval based on the properties of peak elements (i.e., elements greater than their neighbors).
• Handle cases where the peak element may appear at the beginning, end, or middle of the array.

https://leetcode.com/problems/search-in-rotated-sorted-array/

• Divide the array into two parts and determine which part is sorted to adjust the search interval accordingly.
• Handle cases where the target element may be present in the sorted or rotated part of the array.

Full example you can find on Github.